The glide path of asset allocation

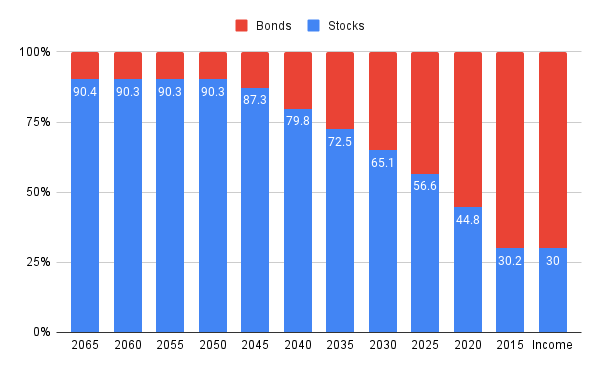
An asset allocation is the percentage for each asset in a portfolio. Suppose a portfolio is investing for retirement, then as an investor’s age nears the retirement age, the percentages should be adjusted. This change over time is called the glide path of an asset allocation.

At the beginning of an investor’s retirement investing career, the risk tolerance, in general, tend to be high. Here an aggressive asset allocation is suitable. As an investor’s age nears the retirement age, the risk of portfolio should be adjusted lower and lower. This makes sense because, at the retirement date, withdrawals (sometimes significant amounts) would be started. Naturally, there is some expectations that the balance is stable. For example, the withdrawals are going to pay for living expenses. Hence a more conservative asset allocation is suitable near the retirement age.

Fortunately, there are mutual funds that manages this transition for an investor. Many mutual fund companies^{1 2 3} offer target-year mutual funds. They automatically implement a glide path. For those who manage their own portfolio, let’s analyze one such glide path.

The chart at the top shows the glide path of Vanguard target date funds. For each fund on the x-axis, the charts show the portion of stocks and bonds. The name of the funds is a year, which is the target year of retirement.

We can observe the following:

1. The glide path starts in 2050 and ends in 2015, for a total of 35 years.
2. This data is from 2022. In other words, somewhere between the 2025 and the 2020 funds. If 2022 is the retirement year, the glide path does not end but continues to 2015.
3. The rate of change increases as the year 2015 gets closer.